Creatinine - Wikipedia, the free encyclopedia - Sent Using Google Toolbar

Creatinine - Wikipedia, the free encyclopedia

Creatinine

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article needs additional citations for verification. Please help improve this article by adding reliable references. Unsourced material may be challenged and removed. (March 2007)

Creatinine
IUPAC name	2-amino-1-methyl-5H-imidazol-4-one
Identifiers
CAS number	[60-27-5]
PubChem	588
MeSH	Creatinine
SMILES	CN1CC(=O)N=C1N
Properties
Molecular formula	C4H7N3O
Molar mass	113.118
Appearance	Solid
Density	1.09 g/cm3
Melting point	300 °C
Hazards
NFPA 704	1 1 0
S-phrases	S24/25
Except where noted otherwise, data are given for materials in their standard state (at 25 °C, 100 kPa) Infobox disclaimer and references

Creatinine is a break-down product of creatine phosphate in muscle, and is usually produced at a fairly constant rate by the body (depending on muscle mass).

Contents [hide] 1 Physiology 2 Diagnostic use 3 Interpretation 4 CT Scans 5 See also 6 References

[edit] Physiology

Creatinine is mainly filtered by the kidney, though a small amount is actively secreted. There is little-to-no tubular reabsorption of creatinine. If the filtering of the kidney is deficient, blood levels rise. As a result, creatinine levels in blood and urine may be used to calculate the creatinine clearance(ClCr), which reflects the glomerular filtration rate (GFR). The GFR is clinically important because it is a measurement of renal function. However, in cases of severe renal dysfunction, the creatinine clearance rate will be "overestimated" because the active secretion of creatinine will account for a larger fraction of the total creatinine cleared. Ketoacids, cimetidine and trimethoprim reduce creatinine tubular secretion and therefore increase the accuracy of the GFR estimate, particularly in severe renal dysfunction. (In the absence of secretion, creatinine behaves like inulin.) A more complete estimation of renal function can be made when interpreting the blood (plasma) concentration of creatinine along with that of urea. In the USA, urea concentration is given as blood urea nitrogen, in mg/In other countries, including those of Europe, urea concentration is measured and quoted in mmol/L. BUN-to-creatinine ratio; ratio of urea to creatinine can indicate other problems besides those intrinsic to the kidney for example, a urea level raised out of proportion to the creatinine may indicate a pre-renal problem such as dehydration. Men tend to have higher levels of creatinine because they have more skeletal muscle than women. Vegetarians tend to have lower creatinine levels, because vegetables contain no creatinine.

[edit] Diagnostic use

Measuring serum creatinine is a simple test and it is the most commonly used indicator of renal function. A rise in blood creatinine levels is observed only with marked damage to functioning nephrons. Therefore, this test is not suitable for detecting early stage kidney disease. A better estimation of kidney function is given by the creatinine clearance test. Creatinine clearance can be accurately calculated using serum creatinine concentration and some or all of the following variables: sex, age, weight, and race as suggested by the American Diabetes Association without a 24 hour urine collection.^[1] Some laboratories will calculate the ClCr if written on the pathology request form; and, the necessary age, sex, and weight are included in the patient information.

[edit] Interpretation

In the United States, creatinine is typically reported in mg/dL, while in Canada and Europe μmol/litre may be used. 1 mg/dL of creatinine is 88.4 μmol/l.

The typical reference ranges are 0.5 to 1.0 mg/dL (about 45-90 μmol/l) for women and 0.7 to 1.2 mg/dL (60-110 μmol/l) for men. While a baseline serum creatinine of 2.0 mg/dL (150 μmol/l) may indicate normal kidney function in a male body builder, a serum creatinine of 0.7 mg/dL (60 μmol/l) can indicate significant renal disease in a frail old woman.

More important than absolute creatinine level is the trend of serum creatinine levels over time.

Creatinine levels may increase when ACE inhibitors (ACEI) or angiotensin-II receptor blockers (ARBs) are used in the treatment of chronic heart failure (CHF). Using both ACEI & ARB concomitantly will increase creatinine levels to a greater degree than either of the two drugs would individually. An increase of <30% is to be expected with ACEI or ARB use.

[edit] CT Scans

The creatinine level is usually measured before performing a contrast-enhanced Computed tomography (CT) scan. In a small proportion of patients the administration of iodine based contrast can cause kidney damage. This may be more likely or severe in patients with an elevated baseline serum creatinine level and, again, in rare cases may require temporary or permanent dialysis. The risk can be reduced somewhat in higher-risk patients by choosing a low-osmolality contrast medium.

[edit] See also

• Cystatin C - novel marker of kidney function.
• Creatinine clearance

[edit] References

1. ^ Gross JL, de Azevedo MJ, Silveiro SP, Canani LH, Caramori ML, Zelmanovitz T (2005). "Diabetic nephropathy: diagnosis, prevention, and treatment". Diabetes Care 28 (1): 164-76. PMID 15616252.

Popular Mechanics - Sent Using Google Toolbar

Popular Mechanics

Inside the Forgotten X Prize—the One That Can Save Your Life

On National DNA Day, PM's resident geek takes the first extensive look at the Archon X Prize in Genomics, the $10 million race for a cheap, disease-hunting gene sequencer that could land on your kitchen counter sooner than you think.

At $150,000 per box, George Church's Polonator device is the smallest and most affordable personal genetic sequencer on the market today. A competition to run through 100 genomes in 10 days for $10,000, however, could change that.

By Erik Sofge

Published on: April 25, 2008

CAMBRIDGE, Mass. — It's an odd-looking gadget—more like a free-standing safe than a self-contained DNA sequencer. This certainly doesn't look like the kind of machine that could prevent diseases and save thousands of lives. And at the moment, the Polonator G.007 isn't even sequencing anyone's DNA. Its belly loaded with dye and front panel opened wide, the arcane inner workings of the box are exposed—not that that's any less confusing, with fluid pumping through snaking, translucent lines. The handy labels on two of the internal containers—marked WATER and WASH—aren't helping much, either.

But that's the beauty of the Polonator, the world's smallest and cheapest available sequencing device, as it rests quietly in the Church Lab here at Harvard Medical School: To operate it, researchers load one cartridge with liquid reagents and two more with DNA, then shut the door. Wave a hand to activate its proximity sensor, and the sequencing run starts—pulsing LED lights, streaming data and a much clearer picture of lineage and inherited disease.

This is the closest you can get to gene sequencing for dummies. And it could also be the ticket to a $10 million purse for the Personal Genome Project (PGx) in one of the most important research competitions to date. Unlike the 100-mpg race for the Progressive Automotive X Prize or the YouTube moonshot of the Google Lunar X Prize, the unheralded Archon X Prize in Genomics has world-changing implications at stake within a decade—or sooner.

"In 10 years, these things will be small enough and cheap enough to have next to your toaster," says Jason Bobe, director of community for PGx. "We'll be sequencing everything—a plant from your garden or an Angus beef steak—to see if it's the real thing."

Bobe is (sort of) kidding, but the history of personal genomics has been one of incredibly rapid progress, thanks in large part to the man who runs this lab, Harvard genetics professor and Human Genome Project originator George Church. "The price has come down by a factor of 1000 in the past two years," he says. "But we have to make it cheaper. If we can reduce volumes by a hundredfold, we can come close to a $1000 genome."

In any discussion of personal genomics, it's easy to get buried by the numbers. For example, to win the Archon X Prize, a research team must sequence 100 individual genomes with an accuracy of more than 99 percent—within 10 days. Each sequence must include at least 98 percent of a genome and cost $10,000 or less. The first group to pull this off by fall 2013 wins $10 million (the same prize money as the AXP but only a third of what Google is offering). The key factors outlined in the rules and emphasized by early entrants are time, accuracy and cost. That's because the goal isn't to simply give a break to the institutions that already perform sequencing—it's to provide every person on the planet with the chance to have their own DNA sequenced, and potentially upend the medical industry.

"If you could sequence the genomes of 1000 patients with Parkinson's," says Marc Hodosh, senior director for the Archon X Prize, "and compare that to the rest of the population, you could recognize which genes are associated with it. Then, pharmaceutical companies could create targeted drugs, preventive pills." In some cases, such as an extreme predisposition to a type of cancer, doctors could possibly even perform a preemptive operation. An accurate genome could also help you avoid the onset of a given disease in less drastic ways, like staying away from certain drugs or eating specific foods.

Companies like 23andme already offer cheap DNA analysis, but they only offer fractional snips rather than full genomes. The X Prize Foundation is calling for at least 98 percent, with sequences that collect more data per genome than anyone has ever attempted, so controlling costs will be paramount. Church tries to use the least expensive reagents possible to bottom out at somewhere close to $10,000 per sequence, and future generations of the Polonator (the one here is his seventh, having sold two boxes for $150,000 each) could require fewer materials per sequencing run.

While he's excited about being one of seven accepted competitors for the X Prize (15 to 20 teams are expected to enter), Church insists that the real goal isn't a $10,000 genome. "There are 6.5 billion people who need their inherited genome done, as well as day-to-day changes," he says. "We need to really bring this down to $1000, or whatever's affordable, so you think nothing of going into a clinic and doing it again." Researchers are aiming for open-source enzymes and better access to equipment to reach that magic $1000 run. PGx spent years turning its cobbled-together, off-the-shelf sequencing gear—including a microscope rigged to two external PC towers—into a marketable, easy-to-use device (click here for complete plans).

Officials at the X Prize foundation agree that the era of practical personal genomics won't arrive until it gets cheaper, with hopes that a winning prototype could drop closer to $1000 after manufacturing and production. Hodosh likened the rapid increase in genome coverage and accuracy to the yearly upgrade cycle of personal computers, so you won't have to wait until 2013 for the first clues or hints of your genetic vulnerabilities. Call it insurance for your body—not a sure thing, but for a week's salary, it might be worth it.

The competition's final deadline, Hodosh admits, may be pushed back; a final deadline is already open-ended—when lives are at stake, research like this is a bit less sporty than, say, building a suborbital space jet. But when a team announces that it's ready for sequencing, the X Prize Foundation will offer one of two time slots during the year (in January or July), while other teams watch and wait like the rest of us. The first to wrestle those imposing numbers into shape—100 genomes, 10 days, $10,000 or less—wins the biggest number of them all. "For the smaller startups, it would be a real nice perk," Hodosh says. "But on the whole, there are teams that are going to spend more than $10 million. Most aren't doing it for the money. It's that Neil Armstrong moment, that Lindbergh moment, that everyone remembers, that paves the way for a new era."

RELATED STORIES

• EXPERTS: Gene Sequencing in Top 50 Inventions of 50 Years

• ANALYSIS: Inside the New Hunt for a Cure to Growing Old

• PM NEWS: DNA Knockout Innovation Wins Medical Nobel

Howstuffworks "How do stock options work?" - Sent Using Google Toolbar

Howstuffworks "How do stock options work?"

How do stock options work?

Inside This Article

1. 

How do stock options work?

2. 

Lots More Information

3. 

See all Financial Planning articles

Job ads in the classifieds mention stock options more and more frequently. Companies are offering this benefit not just to top-paid executives but also to rank-and-file employees. What are stock options? Why are companies offering them? Are employees guaranteed a profit just because they have stock options? The answers to these questions will give you a much better idea about this increasingly popular movement.

Let's start with a simple definition of stock options:

Stock options from your employer give you the right to buy a specific number of shares of your company's stock during a time and at a price that your employer specifies.

Both privately and publicly held companies make options available for several reasons:

• They want to attract and keep good workers.
• They want their employees to feel like owners or partners in the business.
• They want to hire skilled workers by offering compensation that goes beyond a salary. This is especially true in start-up companies that want to hold on to as much cash as possible.

The price the company sets on the stock (called the grant or strike price) is discounted and is usually the market price of the stock at the time the employee is given the options. Since those options cannot be exercised for some time, the hope is that the price of the shares will go up so that selling them later at a higher market price will yield a profit. You can see, then, that unless the company goes out of business or doesn't perform well, offering stock options is a good way to motivate workers to accept jobs and stay on. Those stock options promise potential cash or stock in addition to salary.

Let's look at a real world example to help you understand how this might work. Say Company X gives or grants its employees options to buy 100 shares of stock at $5 a share. The employees can exercise the options starting Aug. 1, 2001. On Aug. 1, 2001, the stock is at $10. Here are the choices for the employee:

• The first thing an employee can do is convert the options to stock, buy it at $5 a share, then turn around and sell all the stock after a waiting period specified in the options' contract. If an employee sells those 100 shares, that's a gain of $5 a share, or $500 in profit.
• Another thing an employee can do is sell some of the stock after the waiting period and keep some to sell later. Again, the employee has to buy the stock at $5 a share first.
• The last choice is to change all the options to stock, buy it at the discounted price and keep it with the idea of selling it later, maybe when each share is worth $15. (Of course, there's no way to tell if that will ever happen.)

Whatever choice an employee makes, though, the options have to be converted to stock, which brings us to another aspect of stock options: the vesting period. In the example with Company X, employees could exercise their options and buy all 100 shares at once if they wanted to. Usually, though, a company will spread out the vesting period, maybe over three or five or 10 years, and let employees buy so many shares according to a schedule. Here's how that might work:

• You get options on 100 shares of stock in your company.
• The vesting schedule for your options is spread out over four years, with one-fourth vested the first year, one-fourth vested the second, one-fourth vested the third, and one-fourth vested the fourth year.
• This means you can buy 25 shares at the grant or strike price the first year, then 25 shares each year after until you're fully vested in the fourth year.

Remember that each year you can buy 25 shares of stock at a discount, then keep it or sell it at the current market value (current stock price). And each year you're going to hope the stock price continues to rise.

Another thing to know about options is that they always have an expiration date: You can exercise your options starting on a certain date and ending on a certain date. If you don't exercise the options within that period, you lose them. And if you are leaving a company, you can only exercise your vested options; you will lose any future vesting.

One question you might have is: How does a privately held company establish a market and grant (strike) price on each share of its stock? This might be especially interesting to know if you are or might be working for a small, privately held company that offers stock options. What the company does is to fix a price that is related to the internal value of the share, and this is established by the company's board of directors through a vote.

Overall, you can see that stock options do have risk, and they are not always better than cash compensation if the company is not successful, but they are becoming a built-in feature in many industries.

For more stock market and investing information, check out the links on the next page.

Option (finance) - Wikipedia, the free encyclopedia - Sent Using Google Toolbar

Option (finance) - Wikipedia, the free encyclopedia

Option (finance)

From Wikipedia, the free encyclopedia

  (Redirected from Stock option)

Jump to: navigation, search

Financial markets

Bond market Fixed income Corporate bond Government bond Municipal bond Bond valuation High-yield debt

Stock market Stock Preferred stock Common stock Registered share Voting share Stock exchange

Foreign exchange market Retail forex

Derivatives market Credit derivative Hybrid security Options Futures Forwards Swaps

Other Markets Commodity market OTC market Real estate market Spot market

Finance series Financial market Financial market participants Corporate finance Personal finance Public finance Banks and Banking Financial regulation

v • d • e

This article is about options traded in financial markets. For other types of options, see Option.

Options are financial instruments that convey the right, but not the obligation, to engage in a future transaction on some underlying security, or in a futures contract. In other words, the holder does not have to exercise this right, unlike a forward or future. For example, buying a call option provides the right to buy a specified quantity of a security at a set strike price at some time on or before expiration, while buying a put option provides the right to sell. Upon the option holder's choice to exercise the option, the party who sold, or wrote, the option must fulfill the terms of the contract.^[1][2]

The theoretical value of an option can be determined by a variety of techniques. These models, which are developed by quantitative analysts, can also predict how the value of the option will change in the face of changing conditions. Hence, the risks associated with trading and owning options can be understood and managed with some degree of precision.

Exchange-traded options form an important class of options which have standardized contract features and trade on public exchanges, facilitating trading among independent parties. Over-the-counter options are traded between private parties, often well-capitalized institutions, that have negotiated separate trading and clearing arrangements with each other. Another important class of options, particularly in the U.S., are employee stock options, which are awarded by a company to their employees as a form of incentive compensation.

Other types of options exist in many financial contracts, for example real estate options are often used to assemble large parcels of land, and prepayment options are usually included in mortgage loans. However, many of the valuation and risk management principles apply across all financial options.

Contents [hide] 1 Contract specifications 2 Types of options 2.1 Option styles 3 Valuation models 3.1 Black Scholes 3.2 Stochastic volatility models 4 Model implementation 4.1 Analytic techniques 4.2 Binomial tree pricing model 4.3 Monte Carlo models 4.4 Finite difference models 4.5 Other models 5 Risks 5.1 Example 5.2 Pin risk 5.3 Counterparty risk 6 Trading 7 The basic trades of traded stock options 7.1 Long Call 7.2 Short Call 7.3 Long Put 7.4 Short Put 8 Option strategies 9 Historical uses of options 10 See also 11 References 12 Further reading 12.1 Business press and web sites 12.2 Academic literature 13 External links

[edit] Contract specifications

Every financial option is a contract between the two counterparties with the terms of the option specified in a term sheet. Option contracts may be quite complicated; however, at minimum, they usually contain the following specifications:^[3]

• whether the option holder has the right to buy (a call option) or the right to sell (a put option)
• the quantity and class of the underlying asset(s) (e.g. 100 shares of XYZ Co. B stock)
• the strike price, also known as the exercise price, which is the price at which the underlying transaction will occur upon exercise
• the expiration date, or expiry, which is the last date the option can be exercised
• the settlement terms, for instance whether the writer must deliver the actual asset on exercise, or may simply tender the equivalent cash amount
• the terms by which the option is quoted in the market, usually a multiplier such as 100, to convert the quoted price into actual premium amount

[edit] Types of options

The primary types of financial options are:

• Exchange traded options (also called "listed options") are a class of exchange traded derivatives. Exchange traded options have standardized contracts, and are settled through a clearing house with fulfillment guaranteed by the credit of the exchange. Since the contracts are standardized, accurate pricing models are often available. Exchange traded options include:^[4][5]

1. stock options,
2. commodity options,
3. bond options and other interest rate options
4. index (equity) options, and
5. options on futures contracts

• Over-the-counter options (OTC options, also called "dealer options") are traded between two private parties, and are not listed on an exchange. The terms of an OTC option are unrestricted and may be individually tailored to meet any business need. In general, at least one of the counterparties to an OTC option is a well-capitalized institution. Option types commonly traded over the counter include:

1. interest rate options
2. currency cross rate options, and
3. options on swaps or swaptions.

• Employee stock options are issued by a company to its employees as compensation.

[edit] Option styles

Main article: Option style

Naming conventions are used to help identify properties common to many different types of options. These include:

• European option - an option that may only be exercised on expiration.
• American option - an option that may be exercised on any trading day on or before expiration.
• Bermudan option - an option that may be exercised only on specified dates on or before expiration.
• Barrier option - any option with the general characteristic that the underlying security's price must reach some trigger level before the exercise can occur.

[edit] Valuation models

The value of an option can be estimated using a variety of quantitative techniques based on the concept of risk neutral pricing and using stochastic calculus. The most basic model is the Black-Scholes model. More sophisticated models are used to model the volatility smile. These models are implemented using a variety of numerical techniques.^[6] In general, standard option valuation models depend on the following factors:

• The current market price of the underlying security,
• the strike price of the option, particularly in relation to the current market price of the underlier (in the money vs. out of the money),
• the cost of holding a position in the underlying security, including interest and dividends,
• the time to expiration together with any restrictions on when exercise may occur, and
• an estimate of the future volatility of the underlying security's price over the life of the option.

More advanced models can require additional factors, such as an estimate of how volatility changes over time and for various underlying price levels, or the dynamics of stochastic interest rates.

The following are some of the principal valuation techniques used in practice to evaluate option contracts.

[edit] Black Scholes

Main article: Black Scholes

The Black-Scholes model was the first quantitative technique to comprehensively and accurately estimate the price for a variety of simple option contracts. By employing the technique of constructing a risk neutral portfolio that replicates the returns of holding an option, Fischer Black and Myron Scholes produced a closed-form solution for a European option's theoretical price.^[7] At the same time, the model generates hedge parameters necessary for effective risk management of option holdings. While the ideas behind Black-Scholes were ground-breaking and eventually led to a Nobel Prize in Economics for Myron Scholes and Robert Merton, the application of the model in actual options trading is clumsy because of the assumptions of continuous (or no) dividend payment, constant volatility, and a constant interest rate. Nevertheless, the Black-Scholes model is still widely used in academic work, and for many financial applications where the model's error is within margin of tolerance.^[8]

[edit] Stochastic volatility models

Main article: Heston model

Since the market crash of 1987, it has been observed that market implied volatility for options of lower strike prices are typically higher than for higher strike prices, suggesting that volatility is stochastic, varying both for time and for the price level of the underlying security. Stochastic volatility models have been developed including one developed by S.L. Heston.^[9] One principal advantage of the Heston model is that it can be solved in closed-form, while other stochastic volatility models require complex numerical models.^[9]

[edit] Model implementation

Once a valuation model has been chosen, there are a number of different techniques used to take the mathematical models to implement the models.

[edit] Analytic techniques

In some cases, one can take the mathematical model and using analytic methods develop closed form solutions. The resulting solutions are useful because they are rapid to calculate.

[edit] Binomial tree pricing model

Main article: Binomial options pricing model

Closely following the derivation of Black and Scholes, John Cox, Stephen Ross and Mark Rubinstein developed the original version of the binomial options pricing model.^{[10] [11]} It models the dynamics of the option's theoretical value for discrete time intervals over the option's duration. The model starts with a binomial tree of discrete future possible underlying stock prices. By constructing a riskless portfolio of an option and stock (as in the Black-Scholes model) a simple formula can be used to find the option price at each node in the tree. This value can approximate the theoretical value produced by Black Scholes, to the desired degree of precision. However, the binomial model is considered more accurate than Black-Scholes because it is more flexible, e.g. discrete future dividend payments can be modeled correctly at the proper forward time steps, and American options can be modeled as well as European ones. Binomial models are widely used by professional option traders.

[edit] Monte Carlo models

Main article: Monte Carlo model

For many classes of options, traditional valuation techniques are intractable due to the complexity of the instrument. In these cases, a Monte Carlo approach may often be useful. Rather than attempt to solve the differential equations of motion that describe the option's value in relation to the underlying security's price, a Monte Carlo model determines the value of the option for a set of randomly generated economic scenarios. The resulting sample set yields an expectation value for the option.

[edit] Finite difference models

The equations used to value options can often be expressed in terms of partial differential equations, and once expressed in this form, a finite different model can be derived.

[edit] Other models

Other numerical implementations which have been used to value options include finite element methods.

[edit] Risks

As with all securities, trading options entails the risk of the option's value changing over time. However, unlike traditional securities, the return from holding an option varies non-linearly with the value of the underlier and other factors. Therefore, the risks associated with holding options are more complicated to understand and predict.

In general, the change in the value of an option can be derived from Ito's lemma as:

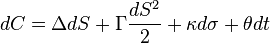
where the greeks Δ, Γ, κ and θ are the standard hedge parameters calculated from an option valuation model, such as Black-Scholes, and dS, dσ and dt are unit changes in the underlier price, the underlier volatility and time, respectively.

Thus, at any point in time, one can estimate the risk inherent in holding an option by calculating its hedge parameters and then estimating the expected change in the model inputs, dS, dσ and dt, provided the changes in these values are small. This technique can be used effectively to understand and manage the risks associated with standard options. For instance, by offsetting a holding in an option with the quantity − Δ of shares in the underlier, a trader can form a delta neutral portfolio that is hedged from loss for small changes in the underlier price. The corresponding price sensitivity formula for this portfolio Π is:

[edit] Example

A call option expiring in 99 days on 100 shares of XYZ stock is struck at $50, with XYZ currently trading at $48. With future realized volatility over the life of the option estimated at 25%, the theoretical value of the option is $1.89. The hedge parameters Δ, Γ, κ, θ are (0.439, 0.0631, 9.6, and -0.022), respectively. Assume that on the following day, XYZ stock rises to $48.5 and volatility falls to 23.5%. We can calculate the estimated value of the call option by applying the hedge parmeters to the new model inputs as:

Under this scenario, the value of the option increases by $0.0614 to $1.9514, realizing a profit of $6.14. Note that for a delta neutral portfolio, where by the trader had also sold 44 shares of XYZ stock as a hedge, the net loss under the same scenario would be ($15.81).

[edit] Pin risk

Main article: Pin risk

A special situation called pin risk can arise when the underlier closes at or very close to the option's strike value on the last day the option is traded prior to expiration. The option writer (seller) may not know with certainty whether or not the option will actually be exercised or be allowed to expire worthless. Therefore, the option writer may end up with a large, unwanted residual position in the underlier when the markets open on the next trading day after expiration, regardless of their best efforts to avoid such a residual.

[edit] Counterparty risk

A further, often ignored, risk in derivatives such as options is counterparty risk. In an option contract this risk is that the seller won't sell or buy the underlying asset as agreed. The risk can be minimized by using a financially strong intermediary able to make good on the trade, but in a major panic or crash the number of defaults can overwhelm even the strongest intermediaries.

[edit] Trading

The most common way to trade options is via standardized options contracts that are listed by various futures and options exchanges. ^[12] By publishing continuous, live markets for option prices, an exchange enables independent parties to engage in price discovery and execute transactions. As an intermediary to both sides of the transaction, the benefits the exchange provides to the transaction include:

• fulfillment of the contract is backed by the credit of the exchange, which typically has the highest rating (AAA),
• counterparties remain anonymous,
• enforcement of market regulation to ensure fairness and transparency, and
• maintenance of orderly markets, especially during fast trading conditions.

Over-the-counter options contracts are not traded on exchanges, but instead between two independent parties. Ordinarily, at least one of the counterparties is a well-capitalized institution. By avoiding an exchange, users of OTC options can narrowly tailor the terms of the option contract to suit individual business requirements. In addition, OTC option transactions generally do not need to be advertised to the market and face little or no regulatory requirements. However, OTC counterparties must establish credit lines with each other, and conform to each others clearing and settlement procedures.

With few exceptions,^[13] there are no secondary markets for employee stock options. These must either be exercised by the original grantee or allowed to expire worthless.

[edit] The basic trades of traded stock options

These trades are described from the point of view of a speculator. If they are combined with other positions, they can also be used in hedging.

[edit] Long Call

Payoffs and profits from a long call.

A trader who believes that a stock's price will increase might buy the right to purchase the stock (a call option) rather than just buy the stock. He would have no obligation to buy the stock, only the right to do so until the expiration date. If the stock price increases over the exercise price by more than the premium paid, he will profit. If the stock price decreases, he will let the call contract expire worthless, and only lose the amount of the premium. A trader might buy the option instead of shares, because for the same amount of money, he can obtain a larger number of options than shares. If the stock rises, he will thus realize a larger gain than if he had purchased shares.

[edit] Short Call

Payoffs and profits from a naked short call.

A trader who believes that a stock price will decrease, can sell the stock short or instead sell, or "write," a call. Because both strategies expose the investor to unlimited losses, they are generally considered inappropriate for small investors. The trader selling a call has an obligation to sell the stock to the call buyer at the buyer's option. If the stock price decreases, the short call position will make a profit in the amount of the premium. If the stock price increases over the exercise price by more than the amount of the premium, the short will lose money, with the potential loss unlimited.

[edit] Long Put

Payoffs and profits from a long put.

A trader who believes that a stock's price will decrease can buy the right to sell the stock at a fixed price (a put option). He will be under no obligation to sell the stock, but has the right to do so until the expiration date. If the stock price decreases below the exercise price by more than the premium paid, he will profit. If the stock price increases, he will just let the put contract expire worthless and only lose his premium paid.

[edit] Short Put

Payoffs and profits from a naked short put.

A trader who believes that a stock price will increase can buy the stock or instead sell a put. The trader selling a put has an obligation to buy the stock from the put buyer at the put buyer's option. If the stock price increases, the short put position will make a profit in the amount of the premium. If the stock price decreases below the exercise price by more than the amount of the premium, the trader will lose money, with the potential loss being up to the full value of the stock.

[edit] Option strategies

Main article: Option strategies

Payoffs from buying a butterfly spread.

Payoffs from selling a straddle.

Payoffs from a covered call.

Combining any of the four basic kinds of option trades (possibly with different exercise prices and maturities) and the two basic kinds of stock trades (long and short) allows a variety of options strategies. Simple strategies usually combine only a few trades, while more complicated strategies can combine several.

Strategies are often used to engineer a particular risk profile to movements in the underlying security. For example, buying a butterfly spread (long one X1 call, short two X2 calls, and long one X3 call) allows a trader to profit if the stock price on the expiration date is near the middle exercise price, X2, and does not expose the trader to a large loss.

Selling a straddle (selling both a put and a call at the same exercise price) would give a trader a greater profit than a butterfly if the final stock price is near the exercise price, but might result in a large loss.

One well-known strategy is the covered call, in which a trader buys a stock (or holds a previously-purchased long stock position), and sells a call. If the stock price rises above the exercise price, the call will be exercised and the trader will get a fixed profit. If the stock price falls, the trader will lose money on his stock position, but this will be partially offset by the premium received from selling the call. Overall, the payoffs match the payoffs from selling a put.

[edit] Historical uses of options

Contracts similar to options are believed to have been used since ancient times. In the real estate market, call options have long been used to assemble large parcels of land from separate owners, e.g. a developer pays for the right to buy several adjacent plots, but is not obligated to buy these plots and might not unless he can buy all the plots in the entire parcel. Film or theatrical producers often buy the right — but not the obligation — to dramatize a specific book or script. Lines of credit give the potential borrower the right — but not the obligation — to borrow within a specified time period.

Many choices, or embedded options, have traditionally been included in bond contracts. For example many bonds are convertible into common stock at the buyer's option, or may be called (bought back) at specified prices at the issuer's option. Mortgage borrowers have long had the option to repay the loan early, which corresponds to a callable bond option.

In London, puts and "refusals" (calls) first became well-known trading instruments in the 1690s during the reign of William and Mary.^[14]

Privileges were options sold over the counter in nineteenth century America, with both puts and calls on shares offered by specialized dealers. Their exercise price was fixed at a rounded-off market price on the day or week that the option was bought, and the expiry date was generally three months after purchase. They were not traded in secondary markets.

[edit] See also

• American Stock Exchange
• Chicago Board Options Exchange
• Eurex
• Euronext.liffe
• International Securities Exchange
• NYSE Arca
• Options Industry Council, sponsored by all 6 options exchanges
• Philadelphia Stock Exchange

[edit] References

1. ^ Brealey, Richard A. & Myers, Stewart (2003), Principles of Corporate Finance (7th ed.), McGraw-Hill, Chapter 20 
2. ^ Hull, John C. (2005), Options, Futures and Other Derivatives (excerpt by Fan Zhang) (6th ed.), Prentice-Hall, ISBN 0131499084, <http://fan.zhang.gl/ecref/options> 
3. ^ . "Characteristics and Risks of Standardized Options" (PDF). Options Clearing Corporation. Retrieved on 2007-06-21.
4. ^ Trade CME Products. Chicago Mercantile Exchange. Retrieved on 2007-06-21.
5. ^ ISE Traded Products. International Securites Exchange. Retrieved on 2007-06-21.
6. ^ Reilly, Frank K. & Brown, Keith C. (2003), Investment Analysis and Portfolio Management (7th ed.), Thomson Southwestern, Chapter 23 
7. ^ Black, Fischer and Myron S. Scholes. "The Pricing of Options and Corporate Liabilities," Journal of Political Economy, 81 (3), 637-654 (1973).
8. ^ Hull, John C. (2005), Options, Futures and Other Derivatives (6th ed.), Prentice-Hall, ISBN 0131499084 
9. ^ ^{a b} Jim Gatheral (2006). The Volatility Surface, A Practitioner's Guide. Wiley Finance. ISBN 978-0471792512. 
10. ^ Cox JC, Ross SA and Rubinstein M. 1979. Options pricing: a simplified approach, Journal of Financial Economics, 7:229-263.[1]
11. ^ Cox, John C. & Rubinstein, Mark (1985), Options Markets, Prentice-Hall, Chapter 5 
12. ^ Harris, Larry (2003), Trading and Exchanges, Oxford University Press, pp.26-27 
13. ^ Elinor Mills. "Google unveils unorthodox stock option auction", CNet, 2006-12-12. Retrieved on 2007-06-19. 
14. ^ Smith, B. Mark (2003). History of the Global Stock Market from Ancient Rome to Silicon Valley. University of Chicago Press, p.20. ISBN 0-226-76404-4. 

[edit] Further reading

[edit] Business press and web sites

• Callan Associates. A Review of the CBOE S&P 500 BuyWrite Index (BXM). (October 2006).
• Clary, Isabelle. "Wall Street Spreading the Word on Options -- Derivative Instruments Now Being Pushed as Source of Better Returns, not Just for Hedging." Pensions & Investments. (February 19, 2007).
• Hadi, Mohammed. "Buy-Write Strategy Could Help in Sideways Market." Wall Street Journal. (April 29, 2006) pg. B5.
• Tan, Kopin, "Yield Boost -- Firms Market Covered-call Writing to Up Returns." Barron's, (Oct. 25, 2004).
• Tergesen, Anne. "Taking Cover with Covered Calls." Business Week, (May 21, 2001), pp. 132.
• Michael C. "Getting Started in Options" Wiley, 2007; www.michaelthomsett.com

[edit] Academic literature

• Fischer Black and Myron S. Scholes. "The Pricing of Options and Corporate Liabilities," Journal of Political Economy, 81 (3), 637-654 (1973).
• Feldman, Barry and Dhuv Roy. "Passive Options-Based Investment Strategies: The Case of the CBOE S&P 500 BuyWrite Index." The Journal of Investing, (Summer 2005).
• Kleinert, Hagen, Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4th edition, World Scientific (Singapore, 2004); Paperback ISBN 981-238-107-4 (also available online: PDF-files)
• Hill, Joanne, Venkatesh Balasubramanian, Krag (Buzz) Gregory, and Ingrid Tierens. "Finding Alpha via Covered Index Writing." Financial Analysts Journal. (Sept.-Oct. 2006). pp. 29-46.
• Moran, Matthew. "Risk-adjusted Performance for Derivatives-based Indexes – Tools to Help Stabilize Returns." The Journal of Indexes. (Fourth Quarter, 2002) pp. 34 – 40.
• Reilly, Frank and Keith C. Brown, Investment Analysis and Portfolio Management, 7th edition, Thompson Southwestern, 2003, pp. 994-5.
• Schneeweis, Thomas, and Richard Spurgin. "The Benefits of Index Option-Based Strategies for Institutional Portfolios" The Journal of Alternative Investments, (Spring 2001), pp. 44 - 52.
• Whaley, Robert. "Risk and Return of the CBOE BuyWrite Monthly Index" The Journal of Derivatives, (Winter 2002), pp. 35 - 42.
• Bloss, Michael; Ernst, Dietmar; Häcker Joachim (2008): Derivatives - An authoritative guide to derivatives for financial intermediaries and investors Oldenbourg Verlag München ISBN 978-3-486-58632-9

[edit] External links

• List of equities with options

[hide] v • d • e Derivatives market
Derivative (finance)
Options	Terms: Strike price · Expiration · Open interest · Pin risk Vanilla options: Option styles · Call · Put · Warrants · Fixed income · Employee stock option · FX Exotic options: Asian · Lookback · Barrier · Binary · Swaption · Mountain range Options strategies: Covered call · Naked put · Collar · Straddle · Strangle · Butterfly Options spreads: Bull spread · Bear spread · Calendar spread · Vertical spread · Debit spread · Credit spread Valuation of options: Moneyness · Option time value · Put-call parity · Black-Scholes · Black · Binomial · Simulation
Swaps	Interest rate swap · Total return swap · Equity swap · Credit default swap · Forex swap · Currency swap · Constant maturity swap · Basis swap · Volatility swap · Variance swap
Other derivatives	Credit derivative · Equity derivative · Interest rate derivative · Inflation derivatives

Retrieved from "http://en.wikipedia.org/wiki/Option_%28finance%29"

Categories: Options | Investment | Contract law