DERIVATIVE, INTEREST RATE SWAP, SWAP,SYNTHETIC COLLATERALIZED DEBT OBLIGATION,TOTAL RETURN SWAP

Derivatives/Synthetic Instruments Demystified 

In Politicized Economy, Systemic Counterparty Confusion onOctober 27, 2008 at 4:44 pm

What Is A Derivative?

A derivative is a contract that derives its value by reference to "something else." That something else can be pretty much anything that can be objectively observed and measured. For example, two parties, A and B, could get together and agree to take positions on the Dow Jones Industrial Average (DJIA). That's an index that can be objectively observed and measured. A could agree to pay B the total percentage-wise return on that index from October 31, 2007 to October 31, 2008 multiplied by a notional amount, where that amount is to be paid on October 31, 2008. In exchange, B could agree to make quarterly payments of some percentage of the notional amount (the swap fee) over that same time frame. Let's say the notional amount is $100 (a position that even Joe The Plumber can take on); the swap fee is 10% per annum; and the total return on the DJIA over that period is 15%. It doesn't take Paul Erdős to realize that this leaves B in the money and A out of the money (A pays $15 and receives $10, so he loses $5).

But what if the DJIA didn't gain 15%? What if it tanked 40% instead? In that case, we have to look to our agreement. Our agreement allocated the DJIA's returns to B and fixed payments to A. It didn't mention DJIA loss. The parties can agree to distribute gain and loss in the underlying reference (the DJIA) any way they like: that's the beauty of enforceable contracts. Let's say that under their agreement, B agreed to pay the negative returns in the DJIA multiplied by the notional amount.  If the market tanked 40%, then B would have made the fixed payments of 10% over the life of the agreement, plus another 40% at the end. That leaves him down $50. Bad year for B.

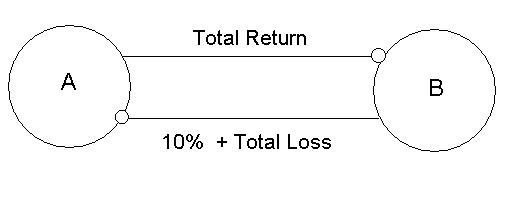
Follow The Money

So what is the net effect of that agreement? B always pays 10% to A, whether the DJIA goes up, down, or stays flat over the relevant time frame. If the DJIA goes up, A has to pay B the percentage-wise returns. If the DJIA goes down, B has to pay A the percentage-wise losses. So, A profits if the DJIA goes down, stays flat, or goes up less than 10% and B profits if the DJIA goes up more than 10%. So, A is short on the DJIA going up 10% and B is long on the DJIA going up 10%. This is accomplished without either of them taking actual ownership of any stocks in the DJIA. We say that A issynthetically shorting the DJIA and B issynthetically long on the DJIA. This type of agreement is called a total return swap(TRS). This TRS exposes A to the risk that the DJIA will appreciate by more than 10% over the life of the agreement and B to the risk that the DJIA will not appreciate by more than 10%.

What Is Risk?

There are a number of competing definitions depending on the context. My own personal view is that risk has two components: (i) the occurrence of an event and (ii) a magnitude associated with that event. This allows us to ask two questions: What is the probability of the event occurring? And if it occurs, what is the expected value of its associated magnitude? We say that P is exposed to a given risk if P expects to incur a gain/loss if the risk-event occurs. For example, in the TRS between A and B, A is exposed to the risk that the DJIA will appreciate by more than 10% over the life of agreement. That risk has two components: the event (the DJIA appreciating by more than 10%) and a magnitude associated with that event (the amount by which it exceeds 10%). In this case, the occurrence of the event and its associated magnitude are equivalent (any non-zero positive value for the magnitude implies that the event occurred) and so our two questions reduce to one question: what is the expected value of the DJIA at the end of the agreement? That obviously depends on who you ask. So, can we then infer that A expects the DJIA to gain less than 10% over the life of the agreement? No, we cannot. If A actually owns $100 worth of the DJIA, A is fully hedged and the agreement is equivalent to bona fide financing. That is, A has no exposure to the DJIA (short on the DJIA through the TRS and long through actually owning it) and makes money only through the swap fee. B's position is the same whether A owns the underlying index or not: B is long on the DJIA, as if he actually owned it. That is, B has synthesized exposure to the DJIA. So, if A is fully hedged the TRS is equivalent to a financing agreement where A "loans" B $100 to buy $100 worth of the DJIA, and then A holds the assets for the life of agreement (like a collateralized loan). As such, B will never agree to pay a swap fee on a TRS that is higher than his cost of financing (since he can just go get a loan and buy the reference asset).

How Derivatives Create, Allocate, And "Transfer" Risk

It is commonly said that derivatives transfer risk. This is not technically true, but often appears to be the case.  Derivatives operate by creating risks that were not present before the parties entered into the derivative contract. For example, assume that A and B enter into an interest rate swap, where A agrees to pay B a fixed annual rate of 8% and B agree to pay A a floating annual rate, say LIBOR, where each is multiplied by a notional amount of $100. Each party agrees to make quarterly payments. Assume that on the first payment date, LIBOR = 4%.  It follows that A owes B $2 and B owes A $1. So, after netting, A pays B $1.

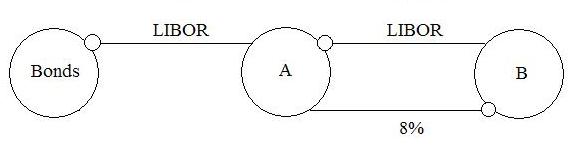
Through the interest rate swap, A is exposed to the risk that LIBOR will fall below 8%. Similarly, B is exposed to the risk that LIBOR will increase above 8%. The derivative contract created these risks and assigned them to A and B respectively. So why do people say that derivatives transfer risk? Assume that A is a corporation and that before A entered into the swap, A issued $100 worth of bonds that pay investors LIBOR annually. By issuing these bonds, A became exposed to the risk that LIBOR would increase by any amount. Assume that the payment dates on the bonds are the same as those under the swap. A's annual cash outflow under the swap is (.08 - LIBOR) x 100. It's annual payments on the bonds are LIBOR x 100. So it's total annual cash outflow under both the bonds and the swap is:

(.08 - LIBOR) x 100 +  LIBOR x 100 = .08 x 100 - LIBOR x 100  + LIBOR x 100 = 8%.

So, A has taken its floating rate LIBOR bonds and effectively transformed them into fixed rate bonds. We say that A has achieved this fixed rate synthetically.

At first glance, it appears as though A has transferred its LIBOR exposure to B through the swap.  This is not technically true. Before A entered into the swap, A was exposed to the risk that LIBOR would increase by any amount. After the swap, A is exposed to the risk that LIBOR will fall under 8%. So, even though A makes fixed payments, it is still exposed to risk: the risk that it will pay above its market rate of financing (LIBOR). For simplicity's sake, assume that B was not exposed to any type of risk before the swap. After the swap, B is exposed to the risk that LIBOR will rise above 8%. This is not the same risk that A was exposed to before the swap (any increase in LIBOR) but it is a similar one (any increase in LIBOR above 8%).

So What Types Of Risk Can Be Allocated Using Derivatives?

Essentially any risk that has an objectively observable event and an objectively measureable associated magnitude can be assigned a financial component and allocated using a derivative contract. There are derivative markets for risks tied to weather, energy products, interest rates, currency, etc. Wherever there is a business or regulatory motivation, financial products will appear to meet the demand. What is important is to realize that all of these products can be analyzed in the same way: identify the risks, and then figure out how they are allocated. This is usally done by simply analyzing the cash flows of the derivative under different sets of assumptions (e.g., the DJIA goes up 15%).

CREDIT DEFAULT SWAP, DERIVATIVE, NETTING,SWAP

Netting Demystified

In Systemic Counterparty Confusion on October 24, 2008 at1:24 am

Netting Is For Everyone, Not Just Fancy Swap Traders

Unlike most terms used in the derivatives world, netting is a good one. It has an intuitive, albeit hokey, feel (unlike other rather sterile terms such as "synthetic collateralized debt obligation"). After all, economics is about human decisions and actions, and as such, it can stand to be a bit hokey. So what is netting? The concept stems from a very simple observation: if I owe you $5 and you owe me $10, you should just give me $5. We could have several debts between the two of us, (e.g., I owe you $2 from Wednesday, $3 from Thursday), but assume we add those up into one debt per person, resulting in one transactional leg (line connecting us) each. In this case, netting would save us a bit of trouble since we only exchange money once, instead of twice.

That Is So Obvious And Trivial That It Can't Be Right

The observation above is indeed an example of the same principle (netting) that is applied to swaps. Our example however, only has 2 parties. The time saved from engaging in 1 transaction instead of 2 is minimal, especially when it's a transaction for such a small amount of money. This is a result of the fact that when there are only 2 parties, let's say you and me, there are only 2 legs to the transaction: the money coming out of me and the money coming out of you. The netting example above reduces that to 1 leg (you pay me). That's called bilateral netting. Again, when there are only 2 parties, the application of netting is simple. But the number of legs increases dramatically as we increase the number of parties (for my fellowgraph theorists, the number of legs is twice the number of edges in a complete graphwith N nodes, where N is the number of parties). For example,  consider the obligations of 3 friends: A, B and C. A owes B $2; A owes C $3; B owes A $4; B owes C $5; C owes A $2; and finally C owes B $6.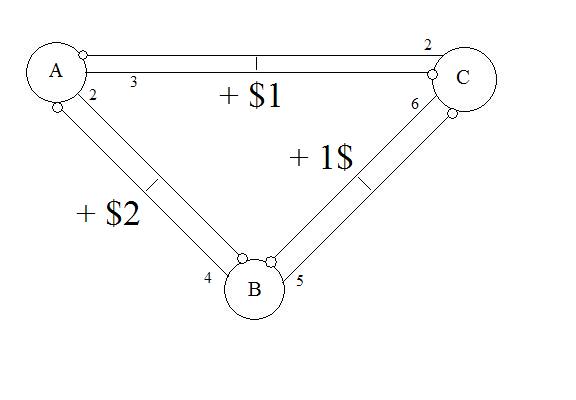

We apply bilateral netting to each of the pairs. That leaves us with the following: A owes C $1; B owes A $2; and C owes B $1. We could just execute 3 transactions and call it a day. But we're smarter than that. We notice that C is basically passing the $1 from A onto B. That is, his inflow is the same as his outflow, so he serves no purpose in our transaction. So, we cut him out of the picture:

Note that the last step we just took, cutting C out, was not bilateral netting. It was a different kind of netting. It required a different observation, but the principle is the same: only engage in necessary transactions. Finally, we apply bilateral netting to the transaction between A and B. So, in the end, that complex sea of relationships boiled down to B paying A $1.

Balsamic Reduction

Rather then execute a disastrously complicated web of transactions, swap dealers, and ordinary banks, use clearing houses to do exactly what we just did above, but on a gigantic scale. Obviously, this is done by an algorithm, and not by hand. Banks, and swap dealers, prefer to strip down the number of transactions so that they only part with their cash when absolutely necessary. There are all kinds of things that can go wrong while your money spins around the globe, and banks and swap dealers would prefer, quite reasonably, to minimize those risks.

An Engine Of Misunderstanding

As you can see from the transactions above, the total amount of outstanding debts is completely meaningless. That complex web of relationships between A, B, and C, reduced to 1 transaction worth $1. Yet, the media would have certainly reported a cataclysmic 2 + 3 + 4 + 5 + 2 + 6 = $22 in total debts.

CREDIT CRISIS, CREDIT CRUNCH, CREDIT DEFAULT SWAP, DERIVATIVE, FINANCE, REGULATION

Systemic Counterparty Confusion: Credit Default Swaps Demystified

In Politicized Economy, Systemic Counterparty Confusion onOctober 23, 2008 at 12:30 am

It Is A Tale Told By An Idiot

The press loves a spectacle. There's a good reason for this: panic increases paranoia, which increases the desire for information, which increases their advertising revenues. Thus, the press has an incentive to exaggerate the importance of the events they report. As such, we shouldn't be surprised to find the press amping up fears about the next threat to the "real economy."

When written about in the popular press, terms such as "derivative" and "mortgage backed security" are almost always preceded by adjectives such as "arcane" and "complex." They're neither arcane nor complex. They're common and straightforward. And the press shouldn't assume that their readers are too dull to at least grasp how these instruments are structured and used. This is especially true of credit default swaps.

Much Ado About Nothing

So what is the big deal about these credit default swaps? Surely, there must be something terrifying and new about them that justifies all this media attention? Actually, there really isn't. That said, all derivatives allow risk to be magnified (which I plan to discuss in a separate article). But risk magnification isn't particular to credit default swaps. In fact, considering the sheer volume of spectacular defaults over the last year, the CDS market has done a damn good job of coping.  Despite wild speculation of impending calamity by the press, the end results have been a yawn . So how is that Reuters went from initially reporting a sensational $365 billion in losses to reporting (12 days later) only $5.2 billion in actual payments? There's a very simple explanation:netting, and the fact that they just don't understand it. As discussed here, the CDS market is a swap market, and as such, the big players in that market aren't interested in taking positions where their capital is at risk. They are interested in making money by creating a market for swaps and pocketing the difference between the prices at which they buy and sell. They are classic middlemen and essentially run an auction house.

Deus Ex Machina

The agreements that document credit default swaps are complex, and in fairness to the press, these are not things we learn about in grammar school - for a more detailed treatment of these agreements, look here. Despite this, the basic mechanics of a credit default swap are easy to grasp. Let's begin by introducing everyone: protection buyer (B) is one party and swap dealer (D) is the other. These two are called swap counterparties or just counterparties for short. Let's first explain what they agree to under a credit default swap, and then afterward, we'll examine why they would agree to it.

What Did You Just Agree To?

Under a typical CDS, the protection buyer, B, agrees to make regular payments (let's say monthly) to the protection seller, D. The amount of the monthly payments, called theswap fee, will be a percentage of the notional amount of their agreement. The term notional amount is simply a label for an amount agreed upon by the parties, the significance of which will become clear as we move on. So what does B get in return for his generosity? That depends on the type of CDS, but for now we will assume that we are dealing with what is called physical delivery. Under physical delivery, if the reference entity defaults, D agrees to (i) accept delivery of certain bonds issued by the reference entity named in the CDS and (ii) pay the notional amount in cash to B. After a default, the agreement terminates and no one makes anymore payments. If default never occurs, the agreement terminates on some scheduled date. The reference entity could be any entity that has debt obligations, like AIG.

Now let's fill in some concrete facts to make things less abstract. Let's assume the reference entity is AIG. And let's assume that the notional amount is $100 million and that the swap fee is at a rate of 6% per annum, or $500,000 per month. Finally, assume that B and D executed their agreement on January 1, 2008 and that B made its first payment on that day.  When February 1, 2008 rolls along, B will make another $500,000 payment. This will go on and on for the life of the agreement, unless AIG triggers a default under the CDS. Again, the agreements are complex and there are a myriad of ways to trigger a default. We consider the most basic scenario in which a default occurs: AIG fails to make a payment on one of its bonds. If that happens, we switch into D's obligations under the CDS. As mentioned above, D has to accept delivery of certain bonds issued by AIG (exactly which bonds are acceptable will be determined by the agreement) and in exchange D must pay B $100 million.

Why Would You Do Such A Thing?

To answer that, we must first observe that there are two possibilities for B's state of affairs before AIG's default: he either (i) owned AIG issued bonds or (ii) he did not. I know, very Zen. Let's assume that B owned $100 million worth of AIG's bonds. If AIG defaults, B gives D his bonds and receives his $100 million in principal (the notional amount). If AIG doesn't default, B pays $500,000 per month over the life of the agreement and collects his $100 million in principal from the bonds when the bonds mature. So in either case, B gets his principal. As a result, he has fully hedged his principal. So, for anyone who owns the underlying bond, a CDS will allow them to protect the principal on that bond in exchange for sacrificing some of the yield on that bond.

Now let's assume that B didn't own the bond. If AIG defaults, B has to go out and buy $100 million par value of AIG bonds. Because AIG just defaulted, that's going to cost a lot less than $100 million. Let's say it costs B $50 million to buy AIG issued bonds with a par value of $100 million. B is going to deliver these bonds to D and receive $100 million. That leaves B with a profit of $50 million. Outstanding. But what if AIG doesn't default? In that case, B has to pay out $500,000 per month for the life of the agreement and receives nothing. So, a CDS allows someone who doesn't own the underlying bond to short the bond. This is called synthetically shorting the bond. Why? Because it sounds awesome.

So why would D enter into a CDS? Again, most of the big protection sellers buy and sell protection and pocket the difference. But, this doesn't have to be the case. D could sell protection without entering into an offsetting transaction. In that case, he has synthetically gone long on the bond. That is, he has almost the same cash flows as someone who owns the bond.